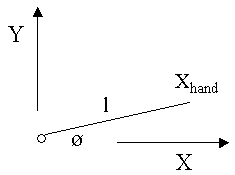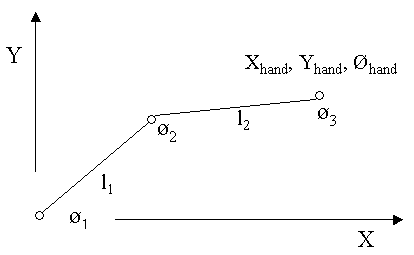|
|
Мы уже видели проблему прямой кинематики . Проблема обратной кинематики значительно более интересна и её решение более полезно.
На уровне позици, проблема звучит так, "Известна требуемая позиция руки робота, каковы углы всех его суставов?"
Человек решает эту проблему все время, даже не думая о ней. Когда вы едите вашу кашу на завтрак, вам нужно посто потянуться и захватить ложкой. Вам не думаете, "моё плеча должно сделать это, мой локоть должен сделать это и т.д." Ниже мы увидим, как роботы должны решить проблему. Начнем с самого простого примера.
|
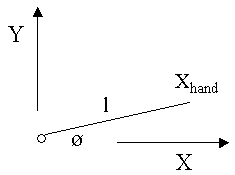
|
|
|
На рисунке вверху схема простого робота, лежащая в плоскости X-Y. Робот имеет звено длиной l
и один сустав с углом Ø. Позиция руки робота Xhand. Проблема обратной кинематики (на уровне позиции) для этого робота следующая: Дано Xhand
каков угол O? Мы начнём решение этой проблемы путём записи уравнения передней позиции, и затем решения для O. |
|
|
|
Xhand = lcosO
(forward position solution) |
|
cosO = Xhand/l |
|
O = cos-1(Xhand/l) |
|
|
|
Чтобы закончить решение, положим, что длина звена роота равна 1 фут мы хотим, чтобы рука робота была в X = 0.7071 футов. Это даёт: |
|
|
O = cos-1(.7071) = +/- 45
градусов |
|
|
Даже в этом простом примере, имеются два решения обратной задачи кинематики: один на плюс 45 градусов и один на уровне минус 45 градусов! Наличие многочисленных решений, добавляет проблем задаче обратной кинематики. Как правило, мы должны знать, какое из решений является правильным. Все языки программирования, что я знаю поддерживают тригонометрическую функцию, которая называется ATan2, которая найдет точный квадрант, если заданы X и Y аргументы: O ATan2 = (Y / X). Теперь у нас есть инструменты, которые нам нужны, чтобы взглянуть на более интересную проблему обратной кинематики:
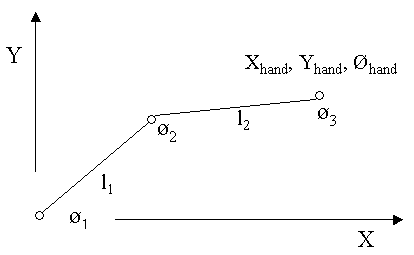
Возможно, вам придется использовать свое воображение немного, но выше, схема плоской части SCARA робота, который мы обсуждали в разделе промышленных роботов . Вот формулировка проблемы обратной кинематики на уровне позицию по этому роботу: |
|
|
|
Дано: Xhand, Yhand,
Ohand |
|
Найти: O1, O2
and O3 |
|
|
|
To aid in solving this problem, I am
going to define an imaginary straight line that extends
from the robot's first joint to its last joint as
follows:
Чтобы помочь в разрешении этой проблемы, я собираюсь определить воображаемую прямую линию, которая простирается от первого сустава робота к его последней суставу следующим образом: |
|
|
|
B: длина воображемой линии |
|
q1: угол между осью X и воображаемой линией |
|
q2: внутренний угол между воображаемой линией и звеном l1 |
|
|
| Тогда мы имеем : |
|
|
|
|
B2 = Xhand2
+ Yhand2
(п теореме Пифагора) |
|
q1 = ATan2(Yhand/Xhand) |
|
q2 = acos[(l12
- l22 + B2)/2l1B]
(по закону косинусов) |
|
O1 = q1
+ q2 |
|
O2 = acos[(l12
+ l22 - B2)/2l1l2]
(по закону косинусов) |
|
O3 = Ohand
- O1 - O2 |
|
|
|
| Это завершает решение для O1, O2 и O3
учитывая Xhand, Yhand, Ohand.
Большинство решений обратной кинематики на уровне положения действует в аналогичной форме. Вы будете использовать ваши знания тригонометрии и геометрии в сочетании с вашим творчеством, чтобы выработать решение. Решение приведенные выше работает для SCARA роботов. Если вы можете себе представить поворот SCARA робота на его стороне, то вы увидите, что решения выше, также работает для позиционирования большинства компонентов шести степеней свободы промышленных роботов тоже.. Обратной кинематики решение для картезианской роботов тривиальна, так как все оси, перпендикулярной по определению и, следовательно, нет сцепления движений. |
|
|
|
|